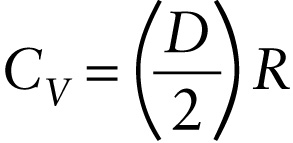Molar specific heat at constant volume for an ideal gas (15-18)
Question 1 of 1
Question
Molar specific heat of an ideal gas at constant pressure
{"title":"Molar specific heat of an ideal gas at constant pressure","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"rect\",\"coords\":\"1,7,42,51\"},{\"shape\":\"poly\",\"coords\":\"144,22\"}]"} {"title":"Ideal gas constant","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"259,6,297,52\"}]"} {"title":"Molar specific heat of an ideal gas at constant volume","description":"Wrong","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"110,6,151,47\"}]"}Review
We'll user the symbol D to represent the number of degrees of freedom. Then the average energy per gas molecule is (D/2)kT. One mole of the gas contains Avogadro's number of molecules, so the energy per mole is NA(D/2)kT=(D/2)(NAk)T=(D/2)RT (Again, recall that k=R/NA, so R=NAk.) Then the internal energy of n moles of ideal gas is
(15-16) U=n(D2R)T (ideal gas, D degrees of freedom)
If the temperature of the gas changes by ΔT, it follows from Equation 16-16 that the internal energy change is
(15-17) ΔU=n(D2R)ΔT (ideal gas, D degrees of freedom)
But we saw above that for an ideal gas, ΔU=nCVΔT. Comparing this to Equation 15-17, we see that